ML&DL&AI/기초통계
분산과 사분위수(Quartile)
Hoon0211
2023. 8. 3. 11:32
728x90
1. 분산
- 관측치들이 평균에서 평균적으로 얼마나 떨어져있는지를 계산
- 분산이 0에 가깝다면 평균 근처에 몰려있다는 것을 의미
- 분산이 커진다면 평균에 멀리 떨어져있다는 것을 의미
- 쉽게 말해 분포되어 있는 정도(흩어진 정도)를 의미

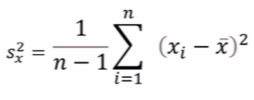
- -, + 부호는 상관없어짐, 분산된 정도를 확인하면 되기때문
- 제곱했을 때 값이 월등히 커지기 때문에 분산의 정도가 확연하게 보임
- 제곱 말고 절댓값을 쓸 수 있지만, 계산할 때 미분가능한 분산 값을 더 선호
- 현실적인 이유
- 평균에서 100명이 100원씩 차이가 날 경우 2명이 5000원씩 차이가 날때
- 절대값 100 x 100원 = 2 x 5,000원 = 10,000원
분산값 100 x (100원)² = 1,000,000원² < 2x (5000원)² = 50,000,000원²
- 표준편차
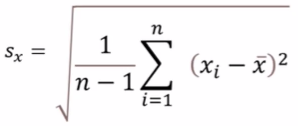
- 분산에 제곱근을 씌워서 단위의 문제를 해결한 숫자
2. 사분위수(Quartile)
- 사분위수는 관측값 오름차순으로 정렬한 후 4개의 동일한 값으로 나눈 값,
관측값의 중심위치와 분포를 쉽고 빠르게 파악가능

3. 상자 그림 ( Boxplot)
- 관측치를 같은 비율로 나누는 지점 계산하여 각 구간의 간격을 살핀다
- ex) 1 6 10 12 12 15 21 22 33 37 56 의 상자그림의 수치는?
- 2사분위수 15
- 중앙값 15이기 때문에
- 중앙값 15이기 때문에
- 1사분위수 11
- 1 ~ 15 의 중앙값
- (10 + 12) / 2 = 11
- 3사분위수 27.5
- 15 ~ 56의 중앙값
- (22 + 23) / 2 = 27.5
- 4분위수 범위 16.5
- 3사분위수 - 1사분위수
- 27.5 - 11 = 16.5
- 최소값 13.75
- 1사분위수 - 1.5 x 4분위수 범위
- 1사분위수 - 1.5 x 4분위수 범위
- 최대값 52.25
- 3사분위수 + 1.5 x 4분위수 범위
- 3사분위수 + 1.5 x 4분위수 범위
- 이상치 56
- 2사분위수 15

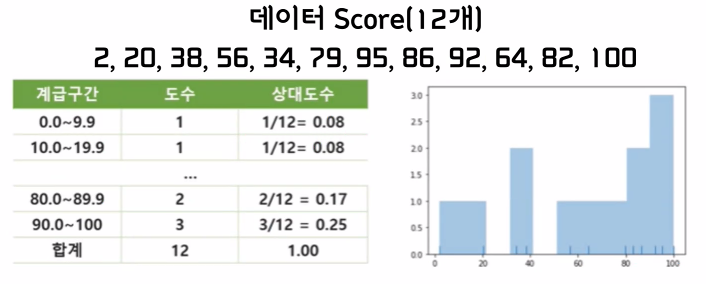
4. 도수분표표와 히스토그램
- 도수분포표
- 범주형 데이터들이 나타내는 빈도수를 정리해 놓은 표
- 범주형 데이터들이 나타내는 빈도수를 정리해 놓은 표
- 히스토그램
- 도수분표를 그래프로 나타낸것
- 도수분표를 그래프로 나타낸것
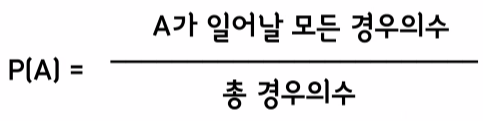
- 확률이란?
728x90