이산확률분포(베르누이, 이항, 포아송)

1. 기본 개념

이산확률분포(Discrete Probability Distribution)

확률변수 X가 취할 수 있는 모든 값을 셀 수 있는 경우, 이를 이산확률변수라고 한다.

이산환률변수의 확률 분포를 의미

 

확률질량함수(Probability Mass Function)

이산확률변수가 특정한 값을 가질 확률을 출력하는 함수

이산 확률 분포를 표현하기 위해 사용하는 확률분포함수로 이해

 

 

2. 이산확률분포

베르누이 시행(Bernoulli Trial)

결과가 두 가지 중 하나로만 나오는 시행을 베르누이 시행이라고 한다.

ex) 자격증 시험 > 합격 또는 불합격

      동전 던지기 > 앞면 또는 뒷면

      합격 또는 꽝만 있는 복권 > 당첨 혹은 꽝

 

베르누이 확률 변수(Bernoulli Random Variable)

베르누이 시행의 결과를 실수 0 또는 1로 나타냅니다.

확률 변수는 0 또는 1의 값만 가질 수 있으므로, 이산 확률 변수입니다.

 

베르누이 확률분포(Bernoulli Distribution)

베르누이 확률변수를 베르누이 확률 분포라고 한다.

확률변수 X가 베르누이 분포를 따른다고 표현하며, 수식으로는 다음과 같이 표현합니다.

X∼Bern(x;μ)
- 모수(parameter)는 세미클론(;) 기호로 구분하여 표기
- 베르누이 확률분포는 모수로 μ를 가지는데, 이 나올 확률을 의미

 

베르누이 분포의 확률질량함수

베르누이 확률 분포의 확률질량 함수는 다음과 같이 표현합니다.

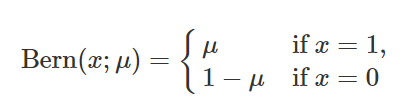
이는 간단히 아래와 같은 하나의 수식으로 표현이 가능합니다.

 

이항 분포

성공 확률이 u인  베르누이 시행을 N번 반복 일때 N번 중에서 성공한 횟수의 확률을 변수 X라고 하며,

X는 0부터 N까지의 정수 중 하나이며 이러한 확률 변수를 이항 분포를 따른다고 한다.

이항 분포는 모수(parameter)로 N과 u를 가진다.
파라미터 1 : 시행 횟수 N
파리미터 2 : 한번의 횟수에서 1이 나올 확률 u

 

이항 분포 확률 변수 X의 확률 질량 함수는 다음과 같습니다.

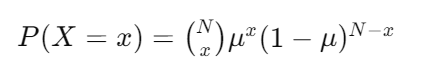
N번의 시행 중에서 xxx번 성공할 수 있는 조합의 수를 나타냈습니다.

u의 확률이 x번 적용을 뜻하며, (1-u)의 확률이 (N - x)번 적용 합니다.

 

포아송(푸아송) 분표(Poisson distribution)

일정한 시간 간격이나 공간 내에서 발생하는 희귀 사건의 수를 모델링할 때 사용한다.

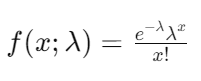
단위 시간에 어떤 사건의 기대 λ일때, 그 사건이 x회 일어날 확률을 구할 수 있다.

예) 1시간 동안의 콜센터에 걸려오는 전화 수, 특정 웹사이트에 1분 동안 방문하는 사용자 수 등