확률 변수와 확률 분포

1. 기본 개념

시행(trial)

반복할 수 있으며, 매번 결과가 달라질 수 있는 실험

ex) 윷을 던지는 행동

 

사건(event)

시행에 따른 결과를 의미

ex) 윳의 결과값 도, 개, 걸, 윷, 모

 

확률(Probability)

어떠한 사건이 일어날 가능성을 수로 표현

ex) 윷을 던져서 모가 나올 확률

1/16

 

 

2. 확률 변수

확률 변수(Random Variable)

사건으로 인해 그 값이 확률적으로 정해지는 변수

윷을 던지는 시행을 할때 나오는 결과가 달라 질 수 있다.

확률 변수 = 윷의 결과

확률 변수는 X라고 표현(확률 변수가 취하는 값은 x)

 

확률 함수(Probabilty Function)

확률 변수에 따라 확률 값을 부여하는 함수

확률 함수는 P라고 표현

P(X=모) = 1/16

- 확률 변수는 함수 일까?
표본 공간(sample space) : 발생 가능한 모든 사건들의 집합(전체 집합)
확률 변수의 역할 : 표본 공간의 사건들을 특정한 수치로 변환하는 함수
상태 공간 (State Space)  : 확률 변수가 취할 수 있는 모든 값의 집합
으로 확률 변수는 함수다

 

 

3. 확률 분포

확률 분포(probabitiy distribution)

사건에 어느 정도의 확률이 할당되었는지 표현한 정보를 의미

확률 분포를 통해 통게적인 특성을 쉽게 이해

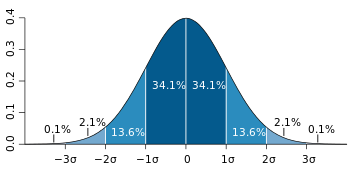
출처 : 위키백과

 

확률 분포 함수(Probabiloty Distribution Function)

확률 변수 X가 가지는 값 x에 확률 P(X = x)을 대응시키는 함수를 의미

확률질량함수 (Probability Mass Function, PMF)와 확률밀도함수 (Probability Density Function, PDF)가 있다.
모든 사건에 대해 확률 분포 함수의 값을 표현한 것을 확률 분포로 이해할 수 있다.

 

- 확률질량함수 (PMF): 이산형 확률 변수가 특정 값들을 가질 확률을 나타내는 함수
- 확률밀도함수 (PDF): 연속형 확률 변수가 특정 값 주변에서의 확률 밀도를 나타내는 함수

 

이산확률분포(Discrete Probability Distribution)

확률변수 X가 취할 수 있는 모든 값을 셀 수 있는 경우, 이를 이산확률변수라고 한다.

이산환률변수의 확률 분포를 의미

이산확률분포 예시
주사위를 던질때 나올 수 있는 수를 확률 변수 X라고 할때
확률 변수 X는 1~6까지 하나의 값을 가질 수 있다.
P(X = 1) = P(X = 2) = P(X = 3) = P(X = 4) = P(X = 5) = P(X = 6) = 1/6 

 

확률질량함수(Probability Mass Function)

이산확률변수가 특정한 값을 가질 확률을 출력하는 함수

이산 확률 분포를 표현하기 위해 사용하는 확률분포함수로 이해

동전 2개를 동시에 던지는 시행에서 두 눈의 합을 X라고 할때
X는 이산확률변수, 확률질량함수 f(x)는 다음과 같다.
f(0) = P(X = 0) = 1/4
f(1) = P(X = 1) = 2/4
f(2) = P(X = 2) = 1/4